Information and modeling systems for the management of large-scale flood situations

A research project is introduced in which a modelling system is being developed to quantify risks of extreme flooding in large river basins. In the system, computer models and modules are coupled together to simulate the functional chain: hydrology – hydraulics – polder diversion – dyke failure – flooding – damage estimate – risk assessment. In order to reduce uncertainty in flood frequency analyses, data sets will be complimented with information from historical chronicles and artwork. Potential worst precipitation and floods will be calculated to indicate possible upper bounds of meteorological and hydrological extremes.
Project description
The concept of the modelling system is illustrated in the figure and consists of the coupling of five models. The hydrology model J2000 (KRAUSE 2000) is used to simulate the runoff generation components to describe the precipitation runoff on the land surfaces. As flooding events become more extreme hydrograph routing of the generated runoff becomes increasingly important, especially in the lowland river reaches. For this, the 1D model RIV1 (ENVIRONMENTAL LABORATORY 1995) which uses the full dynamic wave equation is implemented. A dike breach model (APEL et al. 2004) calculates the probability of a dike failure depending on the condition and type of dike, the failure mechanism (overtopping, piping or underflow) and on the hydraulic load variables in the river, such as water level and water velocity. In the event of a dike breach a 2D storage cell inundation model based on the diffusion wave equation (MERZ 1996) is executed to simulate the movement of water from the breach area into the hinterland. Since the dispersed water also affects the hydraulics in the river, there is an interactive linkage between the dispersion and routing components. A quasi-2D model (1D model DYNHYD (AMBROSE et al. 1993) with a 2D discretisation scheme) simulates peak discharge capping from the main river. The Typed Data Transfer (http://www.pik-potsdam.de/software/tdt) library developed by the Modelling Environment Group at the Potsdam Institute for Climate Impact Research provides a simple interface of data transfer between the computer programs across the computing platforms.
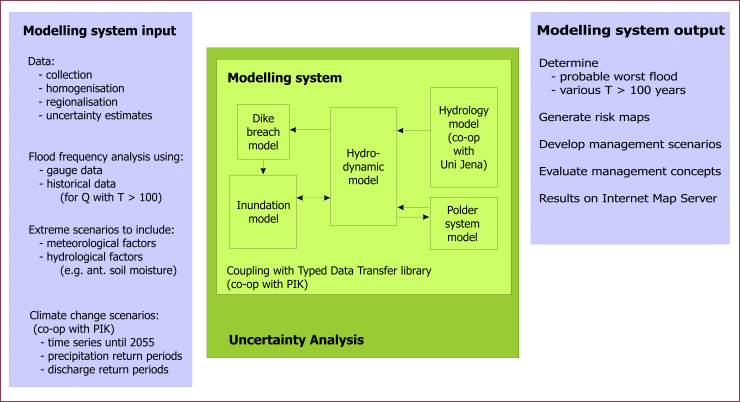
Data is required as input to run the modelling system, which needs to be collected, homogenised and regionalised from point samples to area descriptions. Estimates of the statistical uncertainty in the data and parameter values are required for an uncertainty analysis. Uncertainty analysis includes error propagation due to parameters, boundary conditions and modelling system structure (i.e. processes).
An additional output from the modelling system can also be the simulation of climate change scenarios in which data consisting of trends in meteorological variables until 2055 are used for the simulation. A flood frequency analysis of the future 50 years situation can be compared with the analysis from the past 50 years to record changes in spatial patterns of the flood frequencies in a river catchment. Risk analysis and mapping is also an important output component to aid in the conceptualisation and evaluation of management schemes.
Publications
| Lindenschmidt, K.-E., Fleischbein, K., Petrow, T., Vorogushyn, S., Theobald, S. & Merz, B. (2005) | Model system development and uncertainty for the provisionary management of extreme floods in large river basins | Advances in Geosciences 5: 99-104 | » Link |
| Fleischbein, K., Lindenschmidt, K.-E. & Merz, B. (2006) | Modelling the runoff response in the Mulde catchment (Germany) | Advances in Geosciences 9: 79-84 | » Link |
| Lindenschmidt, K.-E., Herrmann, U., Pech, I. Suhr, U., Apel, H. & Thieken, A.H. (2006) | Risk assessment and mapping of extreme floods in non-dyked communities along the rivers Elbe and Mulde | Advances in Geosciences 9: 1-9 | » Link |
| Huang, S., Rauberg, J., Apel, H. & Lindenschmidt, K.-E. (2007) | The effectiveness of flood discharge capping by proposed polder system constructs along the middle reaches of the Elbe River in Germany | Hydrology and Earth System Sciences Discussions 4: 211-241. | » Link |

